«K12/K13» 60. Hausaufgabe «PDF», «POD»

0.0.1 ↑ 60. Hausaufgabe

0.0.1.1 ↑ Wechselstromkreisanalyse

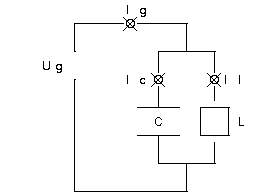
Wechselstromwiderstände von Kondensator und Spule

R_{C_\omega} = \frac{1}{\omega C};$R_{C_{\omega }}=\frac{1}{\omega C};$

R_{L_\omega} = \omega L;$R_{L_{\omega }}=\omega L;$

\omega_0 = \frac{1}{\sqrt{L C}};${\omega }_0=\frac{1}{\sqrt{LC}};$

\hat U_G = \sqrt{2} \, U_{G_{\text{eff}}};${Û}_G=\sqrt{2}{U}_{G_{\text{eff}}};$

Terme für den Gesamtwiderstand und die Ströme I_{G_\omega}(t)$I_{G_{\omega }}\left(t\right)$, I_{C_\omega}(t)$I_{C_{\omega }}\left(t\right)$, I_{L_\omega}(t)$I_{L_{\omega }}\left(t\right)$

⇒ R_\omega = \dfrac{1}{\frac{1}{R_{C_\omega}} + \frac{1}{R_{L_\omega}}} = \dfrac{\omega L}{\omega^2 L C + 1};$R_{\omega }=\frac{1}{\frac{1}{R_{C_{\omega }}}+\frac{1}{R_{L_{\omega }}}}=\frac{\omega L}{{\omega }^{2}LC+1};$

⇒ I_{G_\omega}(t) = \frac{U_{G_\omega}(t)}{R_\omega} = \hat U_G \sin \omega t \cdot \frac{\omega^2 L C + 1}{\omega L};$I_{G_{\omega }}\left(t\right)=\frac{U_{G_{\omega }}\left(t\right)}{R_{\omega }}={Û}_{G}sin\omega t\cdot \frac{{\omega }^{2}LC+1}{\omega L};$

⇒ I_{C_\omega}(t) = \frac{U_{G_\omega}(t)}{R_{C_\omega}} = \hat U_G \sin \omega t \cdot \omega C = \underbrace{\hat U_G \cdot \omega C}_{\hat I_{C_\omega}} \cdot \sin \omega t;$I_{C_{\omega }}\left(t\right)=\frac{U_{G_{\omega }}\left(t\right)}{R_{C_{\omega }}}={Û}_{G}sin\omega t\cdot \omega C=\underset{{Î}_{C_{\omega }}}{\underbrace{{Û}_G\cdot \omega C}}\cdot sin\omega t;$

⇒ I_{L_\omega}(t) = \frac{U_{G_\omega}(t)}{R_{L_\omega}} = \hat U_G \sin \omega t \cdot \frac{1}{\omega L};$I_{L_{\omega }}\left(t\right)=\frac{U_{G_{\omega }}\left(t\right)}{R_{L_{\omega }}}={Û}_{G}sin\omega t\cdot \frac{1}{\omega L};$

Grenzwertbetrachtungen

• Betrachtung des Gesamtwiderstandes R_\omega$R_{\omega }$:

  \lim\limits_{\omega \to 0 \frac{1}{\mathrm{s}}} R_\omega = 0 \,\Omega;$\underset{\omega \to 0\frac{1}{\text{s}}}{lim}{R}_{\omega }=0\Omega ;$ (Einsetzen)

  \lim\limits_{\omega \to \infty \frac{1}{\mathrm{s}}} R_\omega = 0 \,\Omega;$\underset{\omega \to \infty \frac{1}{\text{s}}}{lim}{R}_{\omega }=0\Omega ;$ (Grad des Polynoms des Zählers kleiner als der des Nenners)

  R_{\omega_0} = \dfrac{L}{\sqrt{L C} \left(\frac{1}{LC} LC + 1\right)} = \sqrt{\frac{L}{2 C}};$R_{{\omega }_0}=\frac{L}{\sqrt{LC}\left(\frac{1}{LC}LC+1\right)}=\sqrt{\frac{L}{2C}};$

  Anschaulich: Bei \omega \to 0 \frac{1}{\mathrm{s}}$\omega \to 0\frac{1}{\text{s}}$ liegt Gleichstrom vor; der Kondensator leitet also gar nicht und die Spule ideal. Bei \omega \to \infty \frac{1}{\mathrm{s}}$\omega \to \infty \frac{1}{\text{s}}$ leitet die Spule gar nicht und der Kondensator ideal.

• Betrachtung des Stroms durch den Kondensator C_{L_\omega}(t)$C_{L_{\omega }}\left(t\right)$:

  \lim\limits_{\omega \to 0 \frac{1}{\mathrm{s}}} I_{C_\omega}(t) = 0 \,\mathrm{A};$\underset{\omega \to 0\frac{1}{\text{s}}}{lim}{I}_{C_{\omega }}\left(t\right)=0\text{A};$ (Einsetzen)

  Bei Gleichstrom ist der Kondensator ein Nichtleiter, I_{C_\omega}(t)$I_{C_{\omega }}\left(t\right)$ ist Null.

  \lim\limits_{\omega \to \infty \frac{1}{\mathrm{s}}} I_{C_\omega}(t)$\underset{\omega \to \infty \frac{1}{\text{s}}}{lim}{I}_{C_{\omega }}\left(t\right)$ ist nicht definiert (Sinus konvergiert nicht). Stattdessen Betrachtung von \hat I_{C_\omega}${Î}_{C_{\omega }}$:

  \hat I_{C_\omega} = \hat U_G \cdot \omega C \to \infty \,\mathrm{A}${Î}_{C_{\omega }}={Û}_G\cdot \omega C\to \infty \text{A}$ für \omega \to \infty \frac{1}{\mathrm{s}};$\omega \to \infty \frac{1}{\text{s}};$

  I_{C_{\omega_0}}(t) = \hat U_G \sin \sqrt{\frac{t^2}{LC}} \cdot \sqrt{\frac{C}{L}};$I_{C_{{\omega }_0}}\left(t\right)={Û}_{G}sin\sqrt{\frac{t^2}{LC}}\cdot \sqrt{\frac{C}{L}};$

• Betrachtung des Stroms durch die Spule I_{L_\omega}(t)$I_{L_{\omega }}\left(t\right)$:

  \lim\limits_{\omega \to 0 \frac{1}{\mathrm{s}}} I_{L_\omega}(t) = \lim\limits_{\omega \to 0 \frac{1}{\mathrm{s}}} \frac{\hat U_G}{L} \frac{\sin \omega t}{\omega} = \lim\limits_{\omega \to 0 \frac{1}{\mathrm{s}}} \frac{\hat U_G}{L} \frac{\sin \omega t}{\omega t} \cdot t = \frac{\hat U_G}{L} \cdot t;$\underset{\omega \to 0\frac{1}{\text{s}}}{lim}{I}_{L_{\omega }}\left(t\right)=\underset{\omega \to 0\frac{1}{\text{s}}}{lim}\frac{{Û}_G}{L}\frac{sin\omega t}{\omega }=\underset{\omega \to 0\frac{1}{\text{s}}}{lim}\frac{{Û}_G}{L}\frac{sin\omega t}{\omega t}\cdot t=\frac{{Û}_G}{L}\cdot t;$ (\lim\limits_{x \to 0} \frac{\sin x}{x} = 1$\underset{x\to 0}{lim}\frac{sinx}{x}=1$)

  Damit nimmt der Strom proportional mit der Zeit zu. Dies entspricht unseren Erwartungen: Da die Spule bei Gleichstrom (\omega \to 0 \frac{1}{\mathrm{s}}$\omega \to 0\frac{1}{\text{s}}$) ein idealer Leiter ist, ist ihr Widerstand Null und damit geht der Strom für t \to \infty \,\mathrm{s}$t\to \infty \text{s}$ gegen Unendlich.

  \lim\limits_{\omega \to \infty \frac{1}{\mathrm{s}}} I_{L_\omega}(t) = 0 \,\mathrm{A};$\underset{\omega \to \infty \frac{1}{\text{s}}}{lim}{I}_{L_{\omega }}\left(t\right)=0\text{A};$ (Zähler "schwankt" zwischen -\hat U_G$-{Û}_G$ und \hat U_G${Û}_G$, Nenner geht gegen Unendlich)

  Die Spule ist bei "unendlich frequenten" Wechselstrom ein Nichtleiter.

  I_{L_{\omega_0}}(t) = \hat U_G \sin \sqrt{\frac{t^2}{LC}} \cdot \sqrt{\frac{C}{L}};$I_{L_{{\omega }_0}}\left(t\right)={Û}_{G}sin\sqrt{\frac{t^2}{LC}}\cdot \sqrt{\frac{C}{L}};$

Abschließende Bemerkungen

Im Resonanzfall ist I_{C_{\omega_0}}(t)$I_{C_{{\omega }_0}}\left(t\right)$ für alle Zeitpunkte t$t$ gleich I_{L_{\omega_0}}(t)$I_{L_{{\omega }_0}}\left(t\right)$!

Graph des Gesamtwiderstandes in Abhängigkeit von \omega$\omega$

Interessant ist, dass der Gesamtwiderstand bei \omega = \sqrt{\frac{1}{C}}$\omega =\sqrt{\frac{1}{C}}$ ist (ermittelbar durch den Ansatz R_\omega' = 0 \frac{\mathrm{Vs}}{\mathrm{A}}$R_{\omega }^{\prime }=0\frac{\text{Vs}}{\text{A}}$). Dieses \omega$\omega$ ist nicht von L$L$ abhängig!

Graph der maximalen Generatorstromstärke in Abhängigkeit von \omega$\omega$

Interessant ist, dass die Scheitelstromstärke des Generators bei \omega_0${\omega }_0$ minimal ist (ermittelbar durch den Ansatz \hat I_{G_\omega}' = 0 \,\mathrm{C}${Î}_{G_{\omega }}^{\prime }=0\text{C}$).

Graph der maximalen Energie in Abhängigkeit von \omega$\omega$

E_{\text{max}_\omega} = E_{L_{\text{max}_\omega}} + E_{C_{\text{max}_\omega}} = \frac{1}{2} L \omega^2 \cdot \hat Q^2 \cos^2 \omega t + \frac{1}{2} \frac{1}{C} \cdot \hat Q^2 \sin^2 \omega t = \frac{1}{2} \hat Q^2 \left(\cos^2 \omega t + \sin^2 \omega t\right) \left(L \omega^2 + \frac{1}{C}\right) = \frac{1}{2} \hat Q^2 \left(L \omega^2 + \frac{1}{C}\right);$E_{{\text{max}}_{\omega }}=E_{L_{{\text{max}}_{\omega }}}+E_{C_{{\text{max}}_{\omega }}}=\frac{1}{2}L{\omega }^2\cdot {\widehat{Q}}^2{cos}^2\omega t+\frac{1}{2}\frac{1}{C}\cdot {\widehat{Q}}^2{sin}^2\omega t=\frac{1}{2}{\widehat{Q}}^2\left({cos}^2\omega t+{sin}^2\omega t\right)\left(L{\omega }^2+\frac{1}{C}\right)=\frac{1}{2}{\widehat{Q}}^2\left(L{\omega }^2+\frac{1}{C}\right);$

Also nimmt der maximale Energieinhalt mit größer werdendem \omega$\omega$ zu; es ergibt sich kein Umkehrpunkt.

(Benötigte Zeit: 140 min)