0.0.1 ↑ 52. Hausaufgabe
0.0.1.1 ↑ Buch Seite 162, Aufgabe 3a
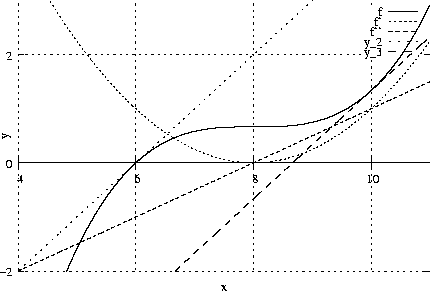
Bestimme Extremwerte und Wendepunkte von G_{\mathrm{f}}! Wie lauten die Gleichungen der Kurventangenten, die mit der positiven x-Achse einen Winkel von 45^\circ bilden?
\mathrm{f}: x \mapsto \mathrm{f}(x) = \frac{1}{12}x^3 - 2x^2 + 16x - 42;
⇒ \mathrm{f}'(x) = \frac{1}{4}x^2 - 4x + 16 = \frac{1}{4}\left(x - 8\right)^2;
⇒ \mathrm{f}''(x) = \frac{1}{2}x - 4 = \frac{1}{2}\left(x - 8\right);
x_1 = 8: \mathrm{f}'(x_1) = 0 \wedge \text{Kein VZW}; ⇒ P_{\mathrm{TEP}}(8, \frac{2}{3});
\mathrm{f}'(x) = 1; \Rightarrow P_2(6, 0); \quad P_3(10, \frac{4}{3});
⇒ \dfrac{y_2}{x - 6} = 1; \Rightarrow y_2 = x - 6; \\ ⇒ \dfrac{y_3 - \frac{4}{3}}{x - 10} = 1; \Rightarrow y_3 = x - \frac{26}{3};