0.0.1 ↑ 55. Hausaufgabe
0.0.1.1 ↑ Buch Seite 163, Aufgabe 14
Gegeben ist \mathrm{f}: x \mapsto \mathrm{f}(x) = \frac{1}{7}\left|x^2 + 3x - 10\right|.
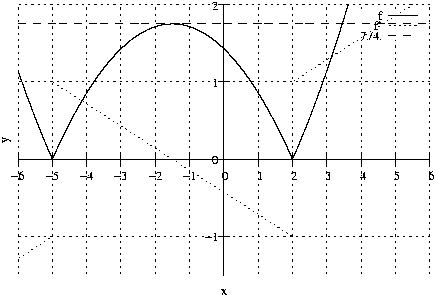
Wo ist \mathrm{f} nicht differenzierbar? Zeichne G_{\mathrm{f}} und G_{\mathrm{f}'} in \left[ -6, 6 \right]! Welche sprunghafte Richtungsänderung erfährt die Tangente beim Überschreiten jener Stellen, an denen die Funktion keine Ableitung hat? Wo ist \mathrm{f}(x) < \frac{7}{4}?
x^2 + 3x - 10 = 0; \Rightarrow x_1 = -5; \quad x_2 = 2;
{} \mathrm{f}'(x) = \begin{cases} {} \frac{1}{7} \left(2x + 3\right) & \text{f"ur } x < -5 \vee x > 2; \\ {} -\frac{1}{7}\left(2x + 3\right) & \text{f"ur } x \in \left] -5, 2 \right[; {} \end{cases}
\lim\limits_{x \to -5\pm} \mathrm{f}'(x) = \mp 1; ⇒ \mathrm{f} ist an -5 nicht diffbar;
\lim\limits_{x \to 2\pm} \mathrm{f}'(x) = \pm 1; ⇒ \mathrm{f} ist an 2 nicht diffbar;
Die Richtungsänderung beträgt jeweils 90^\circ.
\frac{1}{7}\left(x^2 + 3x - 10\right) < \frac{7}{4}; \Rightarrow L = \left] -\dfrac{7\sqrt{2} + 3}{2}, \dfrac{7\sqrt{2} - 3}{2} \right[ \setminus \left\{ -\dfrac{3}{2} \right\};