0.0.1 ↑ 60. Hausaufgabe
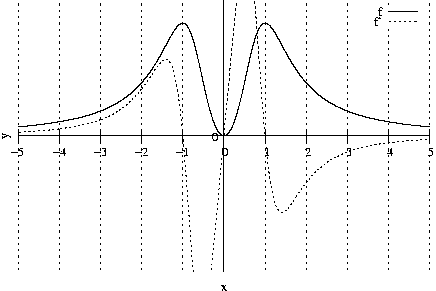
0.0.1.1 ↑ Buch Seite 164, Aufgabe 22c mit W_{\mathrm{f}} und Graph
Bestimme die Wertemengen der folgenden Funktion mit Hilfe der Extremwerte und des Verhaltens an Unendlichkeitsstellen sowie für x \to \pm\infty!
\mathrm{f}: x \mapsto \mathrm{f}(x) = \dfrac{x^2}{x^4 + 1}; \quad D_{\mathrm{f}} = \mathds{R};
\mathrm{f}(x) \to 0 für x \to \infty;
\mathrm{f}'(x) = \dfrac{\left(x^4 + 1\right) \cdot 2x - x^2 \cdot 4x^3}{\left(x^4 + 1\right)^2} = \dfrac{2x^5 + 2x - 4x^5}{\left(x^4 + 1\right)^2} = \dfrac{-2x^5 + 2x}{\left(x^4 + 1\right)} = -2x\dfrac{x^4 - 1}{\left(x^4 + 1\right)^2};
Vorzeichenwechselanalyse gibt:
\mathrm{f} ist sms in \left]-\infty, -1\right] und \left[0, 1\right];
\mathrm{f} ist smf in \left]-1, 0\right[ und \left]1, \infty\right[;
P_{\mathrm{HOP}}(-1, \frac{1}{2});
P_{\mathrm{HOP}}(1, \frac{1}{2});
P_{\mathrm{TIP}}(0, 0);
⇒ W_{\mathrm{f}} = \left[ 0, \frac{1}{2} \right];