«11C» Beschreibung des Sonnensystems «PDF», «POD»

0.0.1 ↑ Beschreibung des Sonnensystems

0.0.1.1 ↑ Ptolemäus (ca. 90-160 n.Chr.): "Almagest"

Geozentrisches Weltbild

0.0.1.2 ↑ Kopernikus (1473-1543)

1. Sonne steht im Mittelpunkt, ruht.

2. Fixsterne sind auf einer kugelförmigen, unermesslich großen, Sphäre angebracht, unbeweglich.

3. Planeten und Erde auf Kreisbahnen um die Sonne

[Galilei 1564-1642]

0.0.1.3 ↑ Johannes Kepler (1571-1630)

(Die ersten zwei Gesetze schon 1609, das dritte Gesetz erst 1619.)

1. Die Planetenbahnen sind Ellipsen, in deren einem Brennpunkt die Sonne steht.

2. Der von der Sonne zum Planeten gezogene Fahrstrahl überstreicht in gleichen Zeiten gleiche Flächen (Flächensatz).

3. Die Quadrate der Umlaufzeiten T$T$ zweier Planeten verhalten sich wie die dritten Potenzen der großen Halbachsen a$a$ ihrer Bahnellipsen.

   \dfrac{T_1^2}{T_2^2} = \dfrac{a_1^3}{a_2^3}; \Rightarrow \dfrac{T_1^2}{a_1^3} = \dfrac{T_2^2}{a_2^3} = C_\odot;$\frac{T_1^2}{T_2^2}=\frac{a_1^3}{a_2^3};\Rightarrow \frac{T_1^2}{a_1^3}=\frac{T_2^2}{a_2^3}=C_{\odot };$

Mittlere Entfernung Erde-Sonne: 1\mathrm{AE} = 1,\!496 \cdot 10^{11}\mathrm{m} \approx 150 \cdot 10^6\mathrm{km};\\$1\text{AE}=1,496\cdot 10^{11}\text{m}\approx 150\cdot 10^6\text{km};$

0.0.1.4 ↑ Satelliten der Erde

In 1000\mathrm{km}$1000\text{km}$ Höhe

Monddaten: r_{\mathrm{Mond}} = 60,\!3R_{\mathrm{Erde}}; \quad T_{\mathrm{Mond}} = 7,\!48 \cdot 10^{-2}\mathrm{a}; \quad r_{\mathrm{Sat}} = 7370\mathrm{km};$r_{\text{Mond}}=60,3R_{\text{Erde}};T_{\text{Mond}}=7,48\cdot 10^{-2}\text{a};r_{\text{Sat}}=7370\text{km};$

\dfrac{T_{\mathrm{Mond}}^2}{T_{\mathrm{Sat}}^2} = \dfrac{a_{\mathrm{Mond}}^3}{a_{\mathrm{Sat}}^3}; \Rightarrow T_{\mathrm{Sat}} = \sqrt{T_{\mathrm{Mond}}^2 \cdot \dfrac{a_{\mathrm{Sat}}^3}{a_{\mathrm{Mond}}^3}} = 1,\!74\mathrm{h};$\frac{T_{\text{Mond}}^2}{T_{\text{Sat}}^2}=\frac{a_{\text{Mond}}^3}{a_{\text{Sat}}^3};\Rightarrow T_{\text{Sat}}=\sqrt{T_{\text{Mond}}^2\cdot \frac{a_{\text{Sat}}^3}{a_{\text{Mond}}^3}}=1,74\text{h};$

Geschwindigkeit: v_{\mathrm{Sat}} = 2\pi \cdot \frac{r_{\mathrm{Sat}}}{T_{\mathrm{Sat}}} = 26613\frac{\mathrm{km}}{\mathrm{h}} = 266 \cdot 10^2 \frac{\mathrm{km}}{\mathrm{h}};$v_{\text{Sat}}=2\pi \cdot \frac{r_{\text{Sat}}}{T_{\text{Sat}}}=26613\frac{\text{km}}{\text{h}}=266\cdot 10^2\frac{\text{km}}{\text{h}};$

Höhe eines Synchronsatelliten

T_{\mathrm{Sat}} = T_{\mathrm{Erde}};$T_{\text{Sat}}=T_{\text{Erde}};$

\dfrac{T_{\mathrm{Mond}}^2}{T_{\mathrm{Sat}}^2} = \dfrac{a_{\mathrm{Mond}}^3}{a_{\mathrm{Sat}}^3}; \Rightarrow a_{\mathrm{Sat}} = \sqrt[3]{a_{\mathrm{Mond}}^3 \cdot \dfrac{T_{\mathrm{Sat}}^2}{T_{\mathrm{Mond}}^2}} = 42344\mathrm{km} = 423 \cdot 10^2\mathrm{km};$\frac{T_{\text{Mond}}^2}{T_{\text{Sat}}^2}=\frac{a_{\text{Mond}}^3}{a_{\text{Sat}}^3};\Rightarrow a_{\text{Sat}}=\sqrt[3]{a_{\text{Mond}}^3\cdot \frac{T_{\text{Sat}}^2}{T_{\text{Mond}}^2}}=42344\text{km}=423\cdot 10^2\text{km};$

Umlaufdauer in Erdnähe (a_{\mathrm{Sat}} \approx R_{\mathrm{Erde}}$a_{\text{Sat}}\approx R_{\text{Erde}}$)

\dfrac{T_{\mathrm{Mond}}^2}{T_{\mathrm{Sat}}^2} = \dfrac{a_{\mathrm{Mond}}^3}{a_{\mathrm{Sat}}^3}; \Rightarrow T_{\mathrm{Sat}} = \sqrt{T_{\mathrm{Mond}}^2 \cdot \dfrac{a_{\mathrm{Sat}}^3}{a_{\mathrm{Mond}}^3}} = 84,\!0\mathrm{min};$\frac{T_{\text{Mond}}^2}{T_{\text{Sat}}^2}=\frac{a_{\text{Mond}}^3}{a_{\text{Sat}}^3};\Rightarrow T_{\text{Sat}}=\sqrt{T_{\text{Mond}}^2\cdot \frac{a_{\text{Sat}}^3}{a_{\text{Mond}}^3}}=84,0\text{min};$

Geschwindigkeit: v_{\mathrm{Sat}} = 2\pi \cdot \frac{r_{\mathrm{Sat}}}{T_{\mathrm{Sat}}} = 7,\!94\frac{\mathrm{km}}{\mathrm{s}};$v_{\text{Sat}}=2\pi \cdot \frac{r_{\text{Sat}}}{T_{\text{Sat}}}=7,94\frac{\text{km}}{\text{s}};$ ("Erste kosmische Geschwindigkeit")

0.0.1.5 ↑ Das Gravitationsgesetz von NEWTON

Mondbewegung: Kreisbahn um Erdmittelpunkt, dazu ist eine Zentripetalkraft nötig

Zugehörige Zentripetalbeschleunigung: \\a_{\mathrm{r}} = \omega^2 r = \dfrac{4\pi^2}{T_{\mathrm{Mond}}^2} r = 2,\!72 \cdot 10^{-3} \frac{\mathrm{m}}{\mathrm{s}^2};$a_{\text{r}}={\omega }^{2}r=\frac{4{\pi }^2}{T_{\text{Mond}}^2}r=2,72\cdot 10^{-3}\frac{\text{m}}{{\text{s}}^2};$

Vergleich mit der Fallbeschleunigung auf der Erde:

\dfrac{g}{a_{\mathrm{r}}} = \dfrac{3600}{1} = \dfrac{r_{\mathrm{Mond}}^2}{R_{\mathrm{Erde}}^2};$\frac{g}{a_{\text{r}}}=\frac{3600}{1}=\frac{r_{\text{Mond}}^2}{R_{\text{Erde}}^2};$

D.h., bei 60-facher Entfernung vom Erdmittelpunkt ist die Beschleunigung nur noch der 60²-te Teil.

⇒ a_{\mathrm{r}} \sim \dfrac{1}{r^2}; \Rightarrow F_{\mathrm{r}} \sim \dfrac{m}{r^2};$a_{\text{r}}\sim \frac{1}{r^2};\Rightarrow F_{\text{r}}\sim \frac{m}{r^2};$

Zweiter Teil: Auch für Planetenbahn: Zentripetalkraft nötig

F_{\mathrm{r}} = m \omega^2 r = \dfrac{4 \pi^2}{T^2} \cdot mr;$F_{\text{r}}=m{\omega }^{2}r=\frac{4{\pi }^2}{T^2}\cdot mr;$

Nach KEPLER: \dfrac{T^2}{r^3} = C_\odot;$\frac{T^2}{r^3}=C_{\odot };$ ⇒ T^2 = r^3 \cdot C_\odot;$T^2=r^3\cdot C_{\odot };$

⇒ F_{\mathrm{r}} = \dfrac{4\pi^2}{r^3 \cdot C_\odot} \cdot mr = \dfrac{4\pi^2}{C_\odot} \dfrac{m}{r^2};$F_{\text{r}}=\frac{4{\pi }^2}{r^3\cdot C_{\odot }}\cdot mr=\frac{4{\pi }^2}{C_{\odot }}\frac{m}{r^2};$

Also auch hier: F_{\mathrm{r}} \sim \frac{m}{r^2};$F_{\text{r}}\sim \frac{m}{r^2};$

Folgerung: Alle Körper ziehen sich gegenseitig an. ⇒ Kraft ist proportional zu den Massen!

F_{\mathrm{r}} = \dfrac{4\pi^2}{C_\odot} \dfrac{m}{r^2} = \dfrac{4 \pi^2}{C_\odot \cdot M_\odot} \dfrac{m \cdot M_\odot}{r^2};$F_{\text{r}}=\frac{4{\pi }^2}{C_{\odot }}\frac{m}{r^2}=\frac{4{\pi }^2}{C_{\odot }\cdot M_{\odot }}\frac{m\cdot M_{\odot }}{r^2};$

Bestimmung von G$G$ durch CAVENDISH 1798: \\G = 6,\!67 \cdot 10^{-11}\, \mathrm{m}^3 \mathrm{kg}^{-1} \mathrm{s}^{-2};$G=6,67\cdot 10^{-11}{\text{m}}^3{\text{kg}}^{-1}{\text{s}}^{-2};$

0.0.1.6 ↑ Massenbestimmung

Erdmasse

\text{Gewichtskraft} = \text{Gravitationskraft}; \Rightarrow\\ mg = G \cdot \dfrac{M_{\mathrm{Erde}} m}{R_{\mathrm{Erde}}^2}; \Rightarrow M_{\mathrm{Erde}} = \dfrac{R_{\mathrm{Erde}}^2 g}{G} = 5,\!97 \cdot 10^{24}\mathrm{kg};$\text{Gewichtskraft}=\text{Gravitationskraft};\Rightarrow mg=G\cdot \frac{M_{\text{Erde}}m}{R_{\text{Erde}}^2};\Rightarrow M_{\text{Erde}}=\frac{R_{\text{Erde}}^{2}g}{G}=5,97\cdot 10^{24}\text{kg};$

Erddichte

\varrho = \dfrac{M_{\mathrm{Erde}}}{V_{\mathrm{Erde}}} = \dfrac{M_{\mathrm{Erde}}}{\frac{4}{3} \pi R_{\mathrm{Erde}}^3} = 5,\!51 \frac{\mathrm{kg}}{\mathrm{dm}^3};$\varrho =\frac{M_{\text{Erde}}}{V_{\text{Erde}}}=\frac{M_{\text{Erde}}}{\frac{4}{3}\pi R_{\text{Erde}}^3}=5,51\frac{\text{kg}}{{\text{dm}}^3};$

0.0.1.7 ↑ Satellitenbahnen (Kreis)

Idee: F_{\mathrm{r}} = F_{\mathrm{Grav}}; \Rightarrow \dfrac{m_{\mathrm{Sat}}v^2}{r} = G \cdot \dfrac{m_{\mathrm{Sat}} M_{\mathrm{Erde}}}{r^2}; \Rightarrow v = \sqrt{G \cdot \dfrac{M_{\mathrm{Erde}}}{r}};$F_{\text{r}}=F_{\text{Grav}};\Rightarrow \frac{m_{\text{Sat}}{v}^2}{r}=G\cdot \frac{m_{\text{Sat}}{M}_{\text{Erde}}}{r^2};\Rightarrow v=\sqrt{G\cdot \frac{M_{\text{Erde}}}{r}};$

Umlaufdauer T$T$: \\v = 2\pi\dfrac{r}{T}; \Rightarrow T = 2 \pi \dfrac{r}{v} = 2\pi\sqrt{\dfrac{r^3}{G \cdot M_{\mathrm{Erde}}}};$v=2\pi \frac{r}{T};\Rightarrow T=2\pi \frac{r}{v}=2\pi \sqrt{\frac{r^3}{G\cdot M_{\text{Erde}}}};$

0.0.1.8 ↑ Berechnung der Mondmasse

F_{\mathrm{r}} = F_{\mathrm{Grav}}; \Rightarrow m_{\mathrm{Mond}} \omega^2 r = G \cdot \dfrac{m_{\mathrm{Mond}} \cdot m_{\mathrm{Erde}}}{r^2};$F_{\text{r}}=F_{\text{Grav}};\Rightarrow m_{\text{Mond}}{\omega }^{2}r=G\cdot \frac{m_{\text{Mond}}\cdot m_{\text{Erde}}}{r^2};$ (ungeeignet!)

Erde und Mond umlaufen einander!

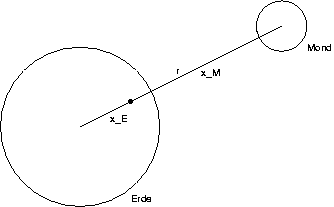
x_{\mathrm{Erde}} + x_{\mathrm{Mond}} = r;$x_{\text{Erde}}+x_{\text{Mond}}=r;$

Zentripetalkräfte der beiden Bewegungen sind gleich (Ursache: Gravitation)

m_{\mathrm{Erde}} \omega^2 x_{\mathrm{Erde}} = m_{\mathrm{Mond}} \omega^2 x_{\mathrm{Mond}}; \Rightarrow m_{\mathrm{Erde}} x_{\mathrm{Erde}} = m_{\mathrm{Mond}} x_{\mathrm{Mond}};$m_{\text{Erde}}{\omega }^2{x}_{\text{Erde}}=m_{\text{Mond}}{\omega }^2{x}_{\text{Mond}};\Rightarrow m_{\text{Erde}}{x}_{\text{Erde}}=m_{\text{Mond}}{x}_{\text{Mond}};$

⇒ m_{\mathrm{Erde}} x_{\mathrm{Erde}} = m_{\mathrm{Mond}} \left(r - x_{\mathrm{Erde}}\right);$m_{\text{Erde}}{x}_{\text{Erde}}=m_{\text{Mond}}\left(r-x_{\text{Erde}}\right);$

Möglichst genaue Werte:

• r = 3,\!844 \cdot 10^8\mathrm{m};$r=3,844\cdot 10^8\text{m};$

• T = 27,\!322 \cdot 86400\mathrm{s};$T=27,322\cdot 86400\text{s};$

• m_{\mathrm{Erde}} = 5,\!976 \cdot 10^{24}\mathrm{kg};$m_{\text{Erde}}=5,976\cdot 10^{24}\text{kg};$

• G = 6,\!672 \cdot 10^{-11}\frac{\mathrm{m}^3}{\mathrm{kg} \mathrm{s}^2};$G=6,672\cdot 10^{-11}\frac{{\text{m}}^3}{\text{kg}{\text{s}}^2};$

Gravitationsgesetz: \\F = G \cdot \dfrac{m_{\mathrm{Erde}} m_{\mathrm{Mond}}}{r^2} = m_{\mathrm{Mond}} \omega^2 x_{\mathrm{Mond}};$F=G\cdot \frac{m_{\text{Erde}}{m}_{\text{Mond}}}{r^2}=m_{\text{Mond}}{\omega }^2{x}_{\text{Mond}};$

⇒ x_{\mathrm{Mond}} = \dfrac{G}{4\pi^2} m_{\mathrm{Erde}} \dfrac{T^2}{r^2} = 3,\!8088 \cdot 10^8\mathrm{m};$x_{\text{Mond}}=\frac{G}{4{\pi }^2}{m}_{\text{Erde}}\frac{T^2}{r^2}=3,8088\cdot 10^8\text{m};$

⇒ x_{\mathrm{Erde}} = r - x_{\mathrm{Mond}} = 3,\!52 \cdot 10^6\mathrm{m};$x_{\text{Erde}}=r-x_{\text{Mond}}=3,52\cdot 10^6\text{m};$

⇒ m_{\mathrm{Mond}} = m_{\mathrm{Erde}} \dfrac{x_{\mathrm{Erde}}}{x_{\mathrm{Mond}}} = 5,\!52 \cdot 10^{22}\mathrm{kg};$m_{\text{Mond}}=m_{\text{Erde}}\frac{x_{\text{Erde}}}{x_{\text{Mond}}}=5,52\cdot 10^{22}\text{kg};$

(Besserer Wert: m_{\mathrm{Mond}} = 7,\!35 \cdot 10^{22}\mathrm{kg};$m_{\text{Mond}}=7,35\cdot 10^{22}\text{kg};$)

0.0.1.9 ↑ Das Gravitationsfeld

Radialsymmetrisches Kraftfeld

ma = F_{\mathrm{G}} = G\dfrac{mM}{r^2};$ma=F_{\text{G}}=G\frac{mM}{r^2};$

⇒ a = \dfrac{F_{\mathrm{G}}}{m} = \dfrac{GM}{r^2};$a=\frac{F_{\text{G}}}{m}=\frac{GM}{r^2};$

⇒ g(r) = \dfrac{G \cdot M}{r^2};$g\left(r\right)=\frac{G\cdot M}{r^2};$ (Definition der Gravitationsfeldstärke)

Hubarbeit und potentielle Energie im Gravitationsfeld

Auf der Erde: Hubarbeit W_{\mathrm{H}} = mgh$W_{\text{H}}=mgh$ bei größerem h$h$ ist g$g$ nicht konstant.

⇒ Intergralrechnung liefert:

W_{\mathrm{H}} = G \cdot mM \left(\dfrac{1}{r_{\mathrm{A}}} - \dfrac{1}{r_{\mathrm{E}}}\right);$W_{\text{H}}=G\cdot mM\left(\frac{1}{r_{\text{A}}}-\frac{1}{r_{\text{E}}}\right);$ (Hubarbeit im Gravitationsfeld)

Arbeit für den Transport "ins Unendliche":

W_\infty = \lim\limits_{r_{\mathrm{E}} \to \infty} G \cdot mM\left(\dfrac{1}{r_{\mathrm{A}}} - \dfrac{1}{r_{\mathrm{E}}}\right) = G \cdot mM \cdot \dfrac{1}{r_{\mathrm{A}}};$W_{\infty }=\underset{r_{\text{E}}\to \infty }{lim}G\cdot mM\left(\frac{1}{r_{\text{A}}}-\frac{1}{r_{\text{E}}}\right)=G\cdot mM\cdot \frac{1}{r_{\text{A}}};$

Beispiel: Geschwindigkeit, um einen Körper von der Erdoberfläche ins Weltall abzuschießen (zweite kosmische Geschwindigkeit).

Ansatz: E_{\mathrm{kin}} = W_\infty; \Rightarrow v = \sqrt{2GM_{\mathrm{E}}R_{\mathrm{E}}^{-1}} = 11,\!2\frac{\mathrm{km}}{\mathrm{s}};$E_{\text{kin}}=W_{\infty };\Rightarrow v=\sqrt{2G{M}_{\text{E}}{R}_{\text{E}}^{-1}}=11,2\frac{\text{km}}{\text{s}};$