«11C» Funktion «PDF», «POD»

1 ↑ Mathematik: Infinitesimalrechnung

1.1 ↑ Schulheft

1.1.1 ↑ Funktion

Unter dem Begriff "Funktion" versteht man eine eindeutige Zuordnung einer Ausgangsmenge (Definitionsmenge \mathds{D}$D$) auf eine Bildmenge (Wertemenge \mathds{W}$W$):

x \in \mathds{D} \longmapsto y \in \mathds{W}$x\in D\mapsto y\in W$

1.1.2 ↑ Typen von mathematischen Funktionen

Polynomfunktionen:

• Konstante Funktion: f\left(x\right) = c$f\left(x\right)=c$

• Lineare Funktion: f\left(x\right) = mx + t$f\left(x\right)=mx+t$

• Quadratische Funktion: f\left(x\right) = ax^2 + bx + c$f\left(x\right)=a{x}^2+bx+c$

• Kubische Funktion: f\left(x\right) = ax^3 + bx^2 + cx + d$f\left(x\right)=a{x}^3+b{x}^2+cx+d$

Exponentialfunktion:

f\left(x\right) = a^x (a > 0)$f\left(x\right)=a^x\left(a>0\right)$

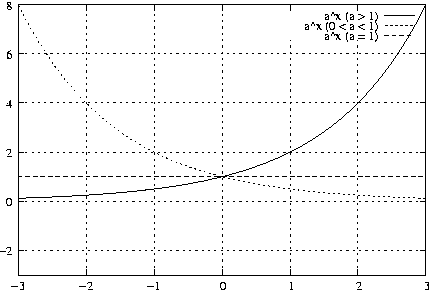
Logarithmusfunktion:

f\left(x\right) = \log_b x$f\left(x\right)={log}_{b}x$ (b \in \mathds{R}^+ \setminus \left\{ 1 \right\}$b\in R^{+}\setminus \left\{1\right\}$)

Wurzelfunktion:

f\left(x\right) = \sqrt{x}$f\left(x\right)=\sqrt{x}$ (\mathds{D} = \mathds{R}_0^+ = \mathds{W}$D=R_0^{+}=W$)

Trigonometrische Funktionen:

• \sin x, \mathds{D} = \mathds{R}$sinx,D=R$

• \cos x, \mathds{D} = \mathds{R}$cosx,D=R$

• \tan x, \mathds{D} = \mathds{R} \setminus \left\{ \frac{\pi}{2} + k\cdot{}\pi, k \in \mathds{Z} \right\}$tanx,D=R\setminus \left\{\frac{\pi }{2}+k\cdot \pi ,k\in Z\right\}$

Gebrochenrationale Funktionen:

Z.B.: \frac{1}{x}$\frac{1}{x}$, \frac{2x}{x^2-1}$\frac{2x}{x^2-1}$, \frac{3x^5-7x}{5x^3+2x+1}$\frac{3x^5-7x}{5x^3+2x+1}$