«11C» Lineare Funktionen «PDF», «POD»

0.0.0.1 ↑ Lineare Funktionen: f\left(x\right) = mx + t$f\left(x\right)=mx+t$

m$m$:

Steigung

t$t$:

y$y$-Abschnitt

Beispiel: f\left(x\right) = \frac{1}{2}x - 2$f\left(x\right)=\frac{1}{2}x-2$

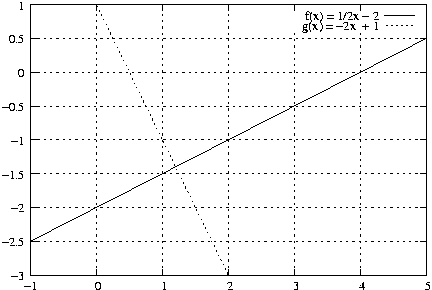
m$m$:

m = \frac{\Delta y}{\Delta x} = \tan \alpha$m=\frac{\Delta y}{\Delta x}=tan\alpha$

Nullstellen:

f\left(x\right) = 0 \Longrightarrow x = 4 \Longrightarrow N\left(4; 0\right)$f\left(x\right)=0\Rightarrow x=4\Rightarrow N\left(4;0\right)$

Schnittpunkt mit y$y$-Achse:

T\left(0; -2\right)$T\left(0;-2\right)$

Aufgabe: Schnittpunkts- und Winkelberechnung zwischen f$f$ und g\left(x\right) = -2x + 1$g\left(x\right)=-2x+1$

Schnittpunkt:

f\left(x\right) = g\left(x\right) \Longrightarrow x = \frac{6}{5}$f\left(x\right)=g\left(x\right)\Rightarrow x=\frac{6}{5}$

Winkel:

{} \tan \left( \arctan m_g - \arctan m_f \right) = {} \tan -\frac{\pi}{2} = {} \text{undefiniert}$tan\left(arctan{m}_g-arctan{m}_f\right)=tan-\frac{\pi }{2}=\text{undefiniert}$

⇒ f$f$ steht senkrecht auf g$g$ (auch wegen m_g = -\frac{1}{m_f}$m_g=-\frac{1}{m_f}$).

0.0.0.2 ↑ Senkrechte Geraden

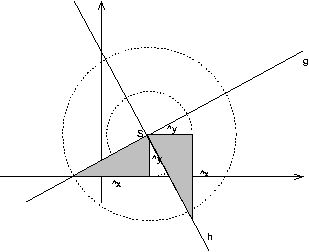
{} m_g = \frac{ \Delta y }{ \Delta x } \\ {} m_h = -\frac{ \Delta x }{ \Delta y } \\$m_g=\frac{\Delta y}{\Delta x}{m}_h=-\frac{\Delta x}{\Delta y}$

⇒ m_g \cdot{} m_h = -1$m_g\cdot m_h=-1$ (Kennzeichen für senkrechte Geraden)

0.0.0.3 ↑ Geradenscharen

Beispiel: g_k: x + y - k = 0; k \in \mathds{R}; \Longrightarrow y = -x + k;$g_k:x+y-k=0;k\in R;\Rightarrow y=-x+k;$ (Parallelenschar)

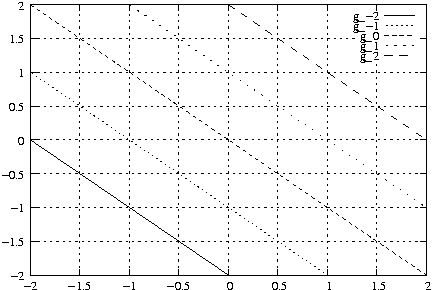
Zusatzaufgabe zur 2. Hausaufgabe:

Nimmt der Flächeninhalt A\left(t\right)$A\left(t\right)$ beliebige Werte aus \mathds{R}_0^+$R_0^{+}$ an?

Untersuchung für t \geq 0$t\ge 0$:

A\left(t\right) = \frac{t^2 + 1}{t}, t \neq 0;$A\left(t\right)=\frac{t^2+1}{t},t\ne 0;$

Untersuchung der Wertemenge von A\left(t\right)$A\left(t\right)$:

Gibt es zu jedem Wert A \in \mathds{R}^+$A\in R^{+}$ einen t$t$-Wert?

{} A = \frac{t^2 + 1}{t}; \Longrightarrow 0 = t^2 - 2At + 1; \Longrightarrow t = \frac{2A \pm 2\sqrt{A^2 - 1}}{2} = A \pm \sqrt{A^2 - 1};$A=\frac{t^2+1}{t};\Rightarrow 0=t^2-2At+1;\Rightarrow t=\frac{2A\pm 2\sqrt{A^2-1}}{2}=A\pm \sqrt{A^2-1};$

A^2 - 1 \geq 0; \Longrightarrow A \geq 1; \Longrightarrow \mathds{W}_A = \left[1; \infty\right[$A^2-1\ge 0;\Rightarrow A\ge 1;\Rightarrow W_A=\left[1;\infty \right[$

⇒ Bei A = 1$A=1$: t = 1$t=1$ ⇒ Neigungswinkel 45^\circ$45^{\circ }$;

0.0.0.4 ↑ Stückweise lineare Funktionen

Die Betragsfunktion x \mapsto \left|x\right| = \begin{cases}x&\text{falls }x \geq 0;\\-x&\text{falls }x < 0;\end{cases}$x\mapsto \left|x\right|=\left\{\begin{array}{cc}x\hfill & \text{falls }x\ge 0;\hfill \\ -x\hfill & \text{falls }x<0;\hfill \end{array}\right.$

Graph:

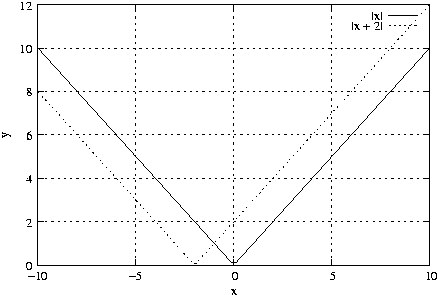
Abwandlungen:

1. f\left(x\right) = \left|x + 2\right| = \begin{cases}-\left(x+2\right)&\text{f"ur }x \leq -2;\\x + 2&\text{f"ur }x > 2;\end{cases}$f\left(x\right)=\left|x+2\right|=\left\{\begin{array}{cc}-\left(x+2\right)\hfill & \text{f”ur }x\le -2;\hfill \\ x+2\hfill & \text{f”ur }x>2;\hfill \end{array}\right.$

0.0.0.5 ↑ Die Signum-Funktion

x \mapsto \mathrm{sgn}\, x = \begin{cases}1 & \text{wenn } x > 0; \\0 & \text{wenn } x = 0; \\ -1 & \text{wenn } x < 0;\end{cases}$x\mapsto \text{sgn}x=\left\{\begin{array}{cc}1\hfill & \text{wenn }x>0;\hfill \\ 0\hfill & \text{wenn }x=0;\hfill \\ -1\hfill & \text{wenn }x<0;\hfill \end{array}\right.$

Zusammenhang: x \cdot \mathrm{sgn}\, x = \left|x\right|$x\cdot \text{sgn}x=\left|x\right|$, x = \left|x\right| \cdot \mathrm{sgn}\, x;$x=\left|x\right|\cdot \text{sgn}x;$