«11C» Umkehrfunktion «PDF», «POD»

0.0.1 ↑ Umkehrfunktion

Ziel: Abbildung rückgänig machen, d.h.: f^{-1}\Bigl( f(x) \Bigr) = x;$f^{-1}\left(f\left(x\right)\right)=x;$

x \in \mathds{D}_f \stackrel{f}{\longrightarrow} y \in \mathds{W}_f = \mathds{D}_{f^{-1}} \stackrel{f^{-1}}{\longrightarrow} x \in \mathds{D}_f = \mathds{W}_{f^{-1}};$x\in D_f\stackrel{f}{\to }y\in W_f=D_{f^{-1}}\stackrel{<msup><mrow>f</mrow><mrow>-1</mrow></msup>}{\to }x\in D_f=W_{f^{-1}};$

Schritte:

1. Auflösen nach x$x$

2. Vertauschen von x$x$ mit y$y$

G_f$G_f$ und G_{f^{-1}}$G_{f^{-1}}$ sind spiegelbildlich bezüglich der Geraden y = x$y=x$.

f$f$ ist umkehrbar.

0.0.1.1 ↑ Umkehrung einer quadratischen Funktion

Beispiel: f(x) = \left(x - 3\right)^2 - 2; \mathds{D}_f = \mathds{R}; \mathds{W}_f = \left[ -2; \infty \right[;$f\left(x\right)={\left(x-3\right)}^2-2;D_f=R;W_f=\left[-2;\infty \right[;$

Auflösen nach x$x$: x = 3 \pm \sqrt{ y + 2 };$x=3\pm \sqrt{y+2};$

⇒ f$f$ ist nicht umkehrbar.

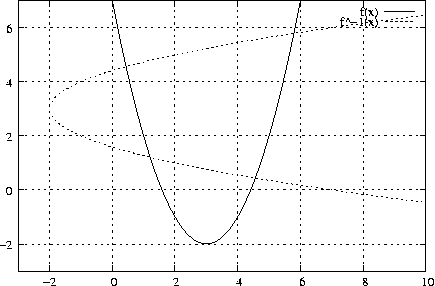
Monotoniekriterium für Umkehrbarkeit:

Eine Funktion ist dann umkehrbar, wenn sie streng monoton ist.

Zerlegung von f$f$ in zwei streng monotone Teile:

• {} f_1(x) = \left(x - 3\right)^2 - 2; \\ {} \mathds{D}_{f_1} = \left] -\infty; 3 \right]; \\ {} \mathds{W}_{f_1} = \left[ -2; \infty \right[;$f_1\left(x\right)={\left(x-3\right)}^2-2;D_{f_1}=\left]-\infty ;3\right];W_{f_1}=\left[-2;\infty \right[;$

• {} f_2(x) = \left(x - 3\right)^2 - 2; \\ {} \mathds{D}_{f_2} = \left] 3; \infty \right]; \\ {} \mathds{W}_{f_2} = \left] -2; \infty \right[;$f_2\left(x\right)={\left(x-3\right)}^2-2;D_{f_2}=\left]3;\infty \right];W_{f_2}=\left]-2;\infty \right[;$

Umkehrung: y = 3 \pm \sqrt{ 2 + x };$y=3\pm \sqrt{2+x};$

• {} f_1^{-1}(x) = 3 - \sqrt{x + 2}; \\ {} \mathds{D}_{f_1^{-1}} = \mathds{W}_{f_1} = \left[ -2; \infty \right[; \\ {} \mathds{W}_{f_1^{-1}} = \mathds{D}_{f_1} = \left] -\infty; 3 \right];$f_1^{-1}\left(x\right)=3-\sqrt{x+2};D_{f_1^{-1}}=W_{f_1}=\left[-2;\infty \right[;W_{f_1^{-1}}=D_{f_1}=\left]-\infty ;3\right];$

• {} f_2^{-1}(x) = 3 + \sqrt{x + 2}; \\ {} \mathds{D}_{f_2^{-1}} = \mathds{W}_{f_2} = \left] -2; \infty \right[; \\ {} \mathds{W}_{f_2^{-1}} = \mathds{D}_{f_2} = \left] 3; \infty \right];$f_2^{-1}\left(x\right)=3+\sqrt{x+2};D_{f_2^{-1}}=W_{f_2}=\left]-2;\infty \right[;W_{f_2^{-1}}=D_{f_2}=\left]3;\infty \right];$