«K12/K13» 10. Hausaufgabe «PDF», «POD»

0.0.1 ↑ 10. Hausaufgabe

0.0.1.1 ↑ Analysis-Buch Seite 37, Aufgabe 33

\mathrm{f}_a(x) := x^3 - ax; \quad D_{\mathrm{f}_a} = \mathds{R}; \quad a \geq 0;${\text{f}}_a\left(x\right):=x^3-ax;D_{{\text{f}}_a}=\mathbb{ℝ};a\ge 0;$

a)

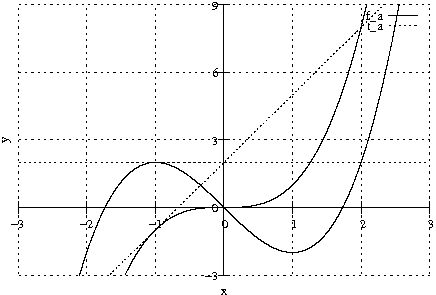
Diskutiere die Kurvenschar (Nullstellen, Extrema, Wendepunkte) und zeichne die Graphen von \mathrm{f}_3${\text{f}}_3$ und \mathrm{f}_0${\text{f}}_0$.

\mathrm{f}_a(x) = x^3 - ax = x\left(x + \sqrt{a}\right)\left(x - \sqrt{a}\right);${\text{f}}_a\left(x\right)=x^3-ax=x\left(x+\sqrt{a}\right)\left(x-\sqrt{a}\right);$

⇒ N_1(0,0); \quad N_2(-\sqrt{a},0); \quad N_3(\sqrt{a},0);$N_1\left(0,0\right);N_2\left(-\sqrt{a},0\right);N_3\left(\sqrt{a},0\right);$

\mathrm{f}_a'(x) = 3x^2 - a = 3\left(x + \sqrt{\frac{a}{3}}\right)\left(x - \sqrt{\frac{a}{3}}\right);${\text{f}}_a^{\prime }\left(x\right)=3x^2-a=3\left(x+\sqrt{\frac{a}{3}}\right)\left(x-\sqrt{\frac{a}{3}}\right);$

⇒ \begin{cases} {} P_{\text{HOP}}\!\left(-\sqrt{\frac{a}{3}}, -\left(\frac{a}{3}\right)^{\frac{3}{2}} + a\sqrt{\frac{a}{3}}\right), \quad P_{\text{TIP}}\!\left(\sqrt{\frac{a}{3}}, \left(\frac{a}{3}\right)^{\frac{3}{2}} - a\sqrt{\frac{a}{3}}\right) & \text{für } a \neq 0; \\ {} P_{\text{TEP}}\!\left(0,0\right) & \text{für } a = 0; \end{cases}$\left\{\begin{array}{cc}{P}_{\text{HOP}}\left(-\sqrt{\frac{a}{3}},-{\left(\frac{a}{3}\right)}^{\frac{3}{2}}+a\sqrt{\frac{a}{3}}\right),P_{\text{TIP}}\left(\sqrt{\frac{a}{3}},{\left(\frac{a}{3}\right)}^{\frac{3}{2}}-a\sqrt{\frac{a}{3}}\right)\hfill & \text{fr }a\ne 0;\hfill \\ P_{\text{TEP}}\left(0,0\right)\hfill & \text{fr }a=0;\hfill \end{array}\right.$

\mathrm{f}_a''(x) = 6x;${\text{f}}_a^{\prime \prime }\left(x\right)=6x;$

⇒ P_{\text{WEP}}(0,0);$P_{\text{WEP}}\left(0,0\right);$

b)

\mathrm{t}_a${\text{t}}_a$ sei die Tangente an G_{\mathrm{f}_a}$G_{{\text{f}}_a}$ im Punkt B(-1, b)$B\left(-1,b\right)$. Berechne den Inhalt des Flächenstücks zwischen \mathrm{t}_a${\text{t}}_a$ und G_{\mathrm{f}_a}$G_{{\text{f}}_a}$ für a = 3$a=3$, a = 0$a=0$ und allgemein.

⇒ \dfrac{\mathrm{t}_a(x) - \mathrm{f}_a(-1)}{x + 1} = \mathrm{f}_a'(-1) = 3 - a; \Rightarrow \mathrm{t}_a(x) = x\left(3 - a\right) + 2;$\frac{{\text{t}}_a\left(x\right)-{\text{f}}_a\left(-1\right)}{x+1}={\text{f}}_a^{\prime }\left(-1\right)=3-a;\Rightarrow {\text{t}}_a\left(x\right)=x\left(3-a\right)+2;$

\mathrm{t}_a(d) = \mathrm{f}_a(d); \Rightarrow 0 = d^3 - 3d - 2 = \left(d - 2\right) \left(d + 1\right)^2;${\text{t}}_a\left(d\right)={\text{f}}_a\left(d\right);\Rightarrow 0=d^3-3d-2=\left(d-2\right){\left(d+1\right)}^2;$

A = \int\limits_{-1}^2 \mathrm{t}_a(x) \,\mathrm{d}x - \int\limits_{-1}^2 \mathrm{f}_a(x) \,\mathrm{d}x = \ldots = \frac{27}{4};$A=\underset{-1}{\overset{2}{\int \; <!--nolimits-->}}{\text{t}}_a\left(x\right)\text{d}x-\underset{-1}{\overset{2}{\int \; <!--nolimits-->}}{\text{f}}_a\left(x\right)\text{d}x=\dots =\frac{27}{4};$

"Einer vons uns beiden ist doof"

"Gehen können so viel wie sie wollen *rausdrück*"

Elementargeometrische Lösung von b) für a = 3$a=3$:

A = 1 \cdot 2 - \int\limits_{-1}^0 \mathrm{f}_3(x) \,\mathrm{d}x + 2 \cdot 2 - \int\limits_{\sqrt{3}}^2 \mathrm{f}_3(x) \,\mathrm{d}x + \int\limits_0^{\sqrt{3}} -\mathrm{f}_3(x) \,\mathrm{d}x = 2 - \frac{5}{4} + 4 - \frac{1}{4} + \frac{9}{4} = \frac{27}{4};$A=1\cdot 2-\underset{-1}{\overset{0}{\int \; <!--nolimits-->}}{\text{f}}_3\left(x\right)\text{d}x+2\cdot 2-\underset{\sqrt{3}}{\overset{2}{\int \; <!--nolimits-->}}{\text{f}}_3\left(x\right)\text{d}x+\underset{0}{\overset{\sqrt{3}}{\int \; <!--nolimits-->}}-{\text{f}}_3\left(x\right)\text{d}x=2-\frac{5}{4}+4-\frac{1}{4}+\frac{9}{4}=\frac{27}{4};$