0.0.1 ↑ Die ideale Batterie?
[Referat von Gawro und mir (gehalten am 6.12.2005); das hier war die Vorlage des Tafelanschriebs, es gab dann kleinere Änderungen; 13 Punkte für Gawro und 14 für mich :)]
0.0.1.1 ↑ Innenwiderstand von Strommessgeräten
Bisher immer angenommen:
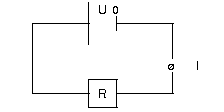
I = I_0 = \frac{U_0}{R_0} = \frac{U_0}{R};
Aber: Messgerät ist nicht ideal; Innenwiderstand!
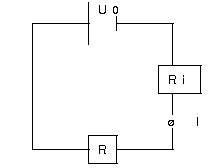
I = I_0 = \dfrac{U_0}{R_0} = \dfrac{U_0}{R + R_{\text{i}}} = \dfrac{U_0}{R \left(1 + \frac{R_{\text{i}}}{R}\right)};
Also: Bei Strommessung Wunsch nach geringem Innenwiderstand
0.0.1.2 ↑ Innenwiderstand von Batterie
Bisher immer angenommen:
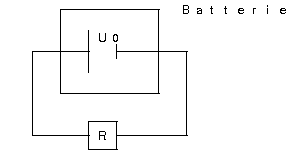
Aber: Batterie ist nicht ideal; Innenwiderstand!
(Konsequenzen bei Kurzschließung einer idealen Batterie: uendlich großer Strom! Unendlich große Energie!)
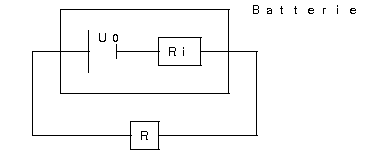
- Allgemein
U_0 = U + U_{\text{i}} = U + R_{\text{i}} I;
- Für Versuch 1
U_0 = U_{\text{V1}} + U_{\text{i},\text{V1}} = U_{\text{V1}} + R_{\text{i},\text{V1}} I_{\text{V1}};
- Für Versuch 2
U_0 = U_{\text{V2}} + U_{\text{i},\text{V2}} = U_{\text{V2}} + R_{\text{i},\text{V2}} I_{\text{V2}};
⇒ R_{\text{i}} = \dfrac{U_{\text{V2}} - U_{\text{V1}}}{I_{\text{V1}} - I_{\text{V2}}};
Sehr interessant: Bei welchem R ist die Leistung maximal?
- Bei idealer Batterie
P(R) = U I(R) = \frac{U^2}{R} = U^2 \frac{1}{R}; →
Also maximale Leistung für R \to 0 \,\Omega (Unendlichkeitsstelle des Graphen von P(R))
- Bei Batterie mit Innenwiderstando
P(R) = U(R) I(R) = \left(U_0 - U_{\text{i}}(R)\right) I(R) = \left(U_0 - R_{\text{i}} I(R)\right) \frac{U_0}{R + R_{\text{i}}} = \frac{U_0^2}{R + R_{\text{i}}} - R_{\text{i}} \frac{U_0^2}{\left(R + R_{\text{i}}\right)^2};
Diskussion des P(R)-Graphen mit Hilfe von P'(R) liefert: maximale Leistung bei R = R_{\text{i}}