0.0.1 ↑ Die Exponentialfunktion
0.0.1.1 ↑ Einführende Beispiele
[...]
Allgemeine Struktur der auftretenden Gleichungen:
\mathrm{f}(x) = \mathrm{f}(x_0) + \mathrm{f}(x_0) k \left(x - x_0\right); \quad x \geq x_0; mit einer Funktion \mathrm{f}{:}\, \mathds{R} \to \mathds{R};
Bemerkungen:
Wird der Zins dem Kapital zugeschlagen, gilt die angegebene Gleichung nur bis zum Zeitpunkt t_Z des Zuschlags. Für t > t_Z muss K(t_0) durch K(t_Z) ersetzt werden.
Für je zwei geeignete Zeitpunkte t_1 und t_2 mit t_1 < t_2 gilt also:
K(t_2) = K(t_1) + K(t_1) k \left(t_2 - t_1\right);
[Einschub:]
\mathrm{f}'(x_0) = \lim\limits_{x \to x_0} \frac{\mathrm{f}(x) - \mathrm{f}(x_0)}{x - x_0};
\mathrm{f}'(x_0) \approx \frac{\mathrm{f}(x) - \mathrm{f}(x_0)}{x - x_0};
\mathrm{f}'(x_0) \cdot \left(x - x_0\right) \approx \mathrm{f}(x) - \mathrm{f}(x_0);
\mathrm{f}'(x_0) \cdot x -\mathrm{f}'(x_0) \cdot x_0 \approx \mathrm{f}(x) - \mathrm{f}(x_0);
\mathrm{f}(x) \approx \underbrace{\mathrm{f}(x_0) + \mathrm{f}'(x_0) x - \mathrm{f}'(x_0) x_0}_{\mathrm{t}(x)};
\mathrm{f}(x) = \sum\limits_{k = 0}^\infty \frac{\mathrm{f}^{(k)}(x_0) \cdot \left(x - x_0\right)^{(k)}}{k!}; (Taylorreihe, [Lagrangereihe bei negativen k])
Auch in den restlichen Beispielen gilt die jeweilige Gleichung für t = t_0 + \Delta t bzw. x = x_0 + \Delta x nur für entsprechend kleine \Delta t bzw. \Delta x. Beim radioaktiven Zerfell etwa muss nach einer Zeitdauer \Delta t \ll \text{Zerfallsdauer} die Zahl der nicht zerfallenen Atome aktualisiert werden.
Überträgt man obige Überlegung auf \mathrm{f}, ergibt sich für beliebige x_1, x_2 unter der Voraussetzung der Differenzierbarkeit
\mathrm{f}(x_2) = \mathrm{f}(x_1) + k \mathrm{f}(x_1) \cdot \left(x_2 - x_1\right);
\lim\limits_{x_2 \to x_1} \frac{\mathrm{f}(x_2) - \mathrm{f}(x_1)}{x_2 - x_1} = \lim\limits_{x_2 \to x_1} k \mathrm{f}(x_1) = k \mathrm{f}(x_1);
0.0.1.2 ↑ Wie sieht der Funktionsterm von \mathrm{f} aus?
Zurück: k = 1;
\mathrm{f}'(x) = \mathrm{f}(x);
Geometrische Bedeutung: Steigung und Funktionswert an einer Stelle sind gleich.
\mathrm{f}(x) = \sum\limits_{k = 0}^\infty a_k x^k = a_0 + \sum\limits_{k = 1}^\infty a_k x^k;
\mathrm{f}'(x) = 0 + \sum\limits_{k = 1}^\infty a_k k x^{k-1} = \sum\limits_{j = 0}^\infty a_{j+1} \left(j + 1\right) x^j;
\mathrm{f}(x) = 1 + x + \frac{x^2}{2} + \frac{x^3}{2 \cdot 3} + \frac{x^4}{2 \cdot 3 \cdot 4} + \cdots = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = \sum\limits_{n = 0}^\infty \frac{x^n}{n!};
\mathrm{f}(x) > 0 für alle x \in \mathds{R};
\mathrm{f}'(x) = \mathrm{f}(x);
\mathrm{f}(0) = 1 = \mathrm{f}'(0);
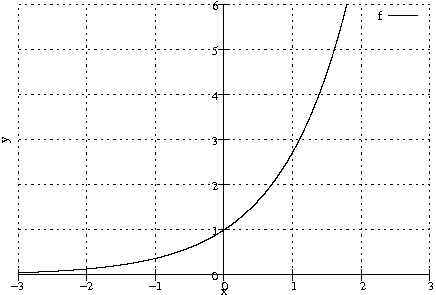
\mathrm{f}(x) lässt sich auch in der Form e^x schreiben, also das Exponentialfunktion mit e = \lim\limits_{\left|x\right| \to \infty} \left(1 + \frac{1}{x}\right)^x (EULERsche Zahl, \approx 2{,}7).
\mathrm{f}{:}\, \mathds{R} \to \mathds{R}^+, \quad x \mapsto e^x (natürliche Exponentialfunktion)
Auch \varphi(x) = a e^x, a \neq 0 erfüllt die Bedingungen.
\lim\limits_{x \to \infty} e^x = \infty
\lim\limits_{x \to -\infty} e^x = 0; (x-Achse ist Asymptote für x \to -\infty)
k \in \mathds{R} \setminus \left\{ 0 \right\};
\mathrm{f}_k(x) = a e^{k x};
\mathrm{f}_k'(x) = a e^{k x} \left(k x\right)' = k a e^{k x} = k \mathrm{f}_k(x);
Rechengesetze für Potenzen vgl. B. S. 77.
0.0.1.3 ↑ Ableitung beliebiger Exponentialfunktionen
\mathrm{g}(x) = b^x; \quad b > 0; x \in \mathds{R};
\mathrm{g}(x) = \left(e^{\ln b}\right)^x = e^{x \cdot \ln b};
\mathrm{g}'(x) = x^{x \cdot \ln b} \cdot \ln b = \left(e^{\ln b}\right)^x \cdot \ln b = b^x \cdot \ln b;