0.0.1 ↑ [Interferenz]
0.0.1.1 ↑ [Das Doppelspaltexperiment]
Anmerkung zu B. S. 133/1
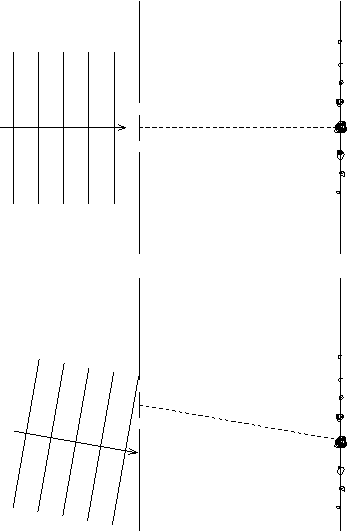
Das Interferenzmuster wandert, ändert sich [aber] qualitativ nicht [nur zieht sich das Muster als Folge des veränderten gedachten "Spaltabstands" leicht auseinander]. Zum Wundern:
[Mehr als nur zwei "Flecke" und nochwas XXX]
0.0.1.1.1 ↑ Interferenzexperiment zur Wellenlängenbestimmung
[Siehe 83. Hausaufgabe.]
0.0.1.1.2 ↑ Ermittlung der Wellenlängen eines Lasers durch Ausmessen des Interferenzmusters
[e: Abstand Laser–Wand, d: Spaltabstand; XXX]
\lambda = \frac{d 1}{n e} = d \frac{a}{e} n^{-1} = \frac{d 1}{e} für n = 1;
\lambda = d \sin\alpha; (Maximumbedingung)
\sin\alpha = \frac{n \lambda}{e};
\tan\alpha = \frac{a}{e};
0.0.1.2 ↑ Zusammenstellung der Gleichungen zur Interferenz (\Delta s = n \lambda → n-tes Maximum bei zwei Strahlen)
[In allen Fällen gibt es keine energetische Wechselwirkung, sondern ausschließlich Impulsaustausch.]
0.0.1.2.3 ↑ Doppelspalt
b \cdot \sin\alpha = n \lambda; → Maximum n-ter Ordnung
b: Spaltabstand
Wegen \sin \alpha \leq 1 gilt: n \leq \frac{b}{\lambda};
Z.B.: \frac{4 \,\mu\mathrm{m}}{630 \,\mathrm{nm}} \approx 6{,}35; → maximal sechs Maxima nach einer Seite, d.h. 13 Maxima [insgesamt]

0.0.1.2.4 ↑ Gitter
b \cdot \sin\alpha = n \lambda; (wie beim Doppelspalt)
b: "Gitterkonstante"
Maxima sind beim Gitter stärker ausgeprägt als beim Doppelspalt.
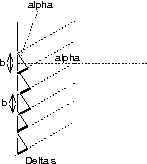
0.0.1.2.5 ↑ Röntgeninterferenz am dreidimensionalen Gitter
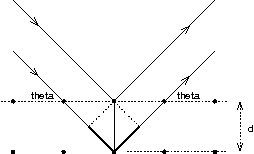
Strahl"ablenkung": 2 \vartheta
2 d \cdot \sin\vartheta = n \lambda;
d: Netzebenenabstand \approx 10^{-10} \,\mathrm{m}
BRAGGreflexe nur unter bestimmten \vartheta–\vartheta-Winkeln!
0.0.1.3 ↑ Anwendung der Drehkristallmethode bei der Analyse von Röntgenstrahlung
Bild 326.1:
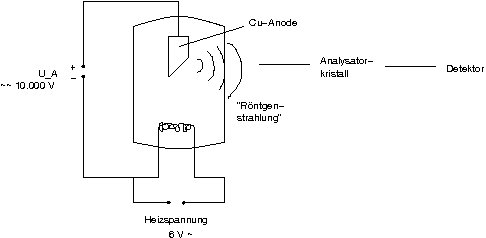
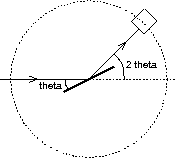
n \lambda = 2 d \sin\vartheta;
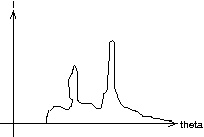
[Echt scharfer Knick im Spektrum, hängt mit der Quantelung der Energieübertragung ab.]
[Charakteristische Peaks, kommen von Elektronen in der Anode, die Schalen wechseln, nachdem andere Elektronen aus dem Kern 'rausgeworfen worden.]