«K12/K13» Zugänge zum Brechungsgesetz «PDF», «POD»

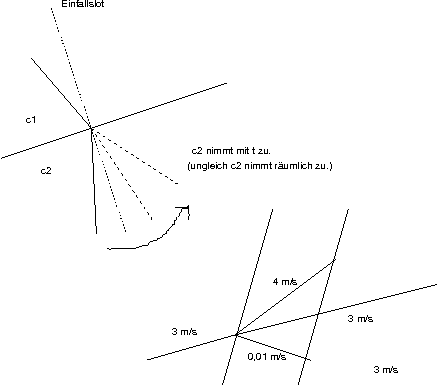
0.0.1 ↑ Zugänge zum Brechungsgesetz

• ["Teilchenmärchen"

  Gesucht ist nicht der räumlich kürzeste, sondern der zeitlich schnellste Weg fürs Photon von A$A$ nach B$B$.

  Problem dabei: Das Photon müsste über übernatürliche Kräfte verfügen, um immer den kürzesten Weg finden zu können.

  

• Licht als Welle

  Betrachtet man dagegen Licht als Welle – delokalisiert – stellen sich diese Probleme nicht:]

  

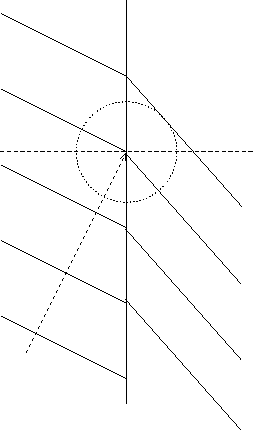
  \lambda_1 = 3 \,\mathrm{LE};${\lambda }_1=3\text{LE};$

  c = \lambda f; \quad f_1 = f_{1,5};$c=\lambda f;f_1=f_{1,5};$

  ⇒ \frac{c_1}{\lambda_1} = \frac{c_{1,5}}{\lambda_{1,5}};$\frac{c_1}{{\lambda }_1}=\frac{c_{1,5}}{{\lambda }_{1,5}};$

  ⇒ \lambda_{1,5} = \frac{c_{1,5}}{c_1} \cdot \lambda_1 = 2 \,\mathrm{LE};${\lambda }_{1,5}=\frac{c_{1,5}}{c_1}\cdot {\lambda }_1=2\text{LE};$

  c_1 = 3 \cdot 10^8 \,\frac{\mathrm{m}}{\mathrm{s}};$c_1=3\cdot 10^8\frac{\text{m}}{\text{s}};$

  c_{1,5} = 2 \cdot 10^8 \,\frac{\mathrm{m}}{\mathrm{s}};$c_{1,5}=2\cdot 10^8\frac{\text{m}}{\text{s}};$

[Da f_1 = f_2$f_1=f_2$ und c_1 \neq c_2$c_1\ne c_2$ und c = \lambda f$c=\lambda f$, muss sich \lambda$\lambda$ beim Übertritt ändern.

"Die Physik muss vor und nach der Brechung die gleiche sein – f_1 = f_2$f_1=f_2$."